
Takagi's nowhere-differentiable function Levy's dragon curve
| E | C | |
| R | S | E |
| H | A | R |
My research is in Probability, Dynamical Systems and Fractal Geometry. This page includes a description of my current and past research interests.
Current research:
Past research:
Through my work
on random probability distributions, which are often of a fractal nature, I
became interested in the field of fractal geometry. Probability theory and
fractal geometry are both firmly rooted in measure theory, and probabilistic
techniques are often used to solve problems in fractal geometry. Hence it seemed
natural to deepen my interest in this subject. My joint work with
Kiko Kawamura involves the
investigation of new classes of fractal functions, as well as fractal functions
which have largely been overlooked by the literature. These include
continuous but nowhere-differentiable functions and
(graph-directed) self-affine functions. In particular, we investigate the degree
of continuity of such functions, the Hausdorff dimensions of their graphs, and
their extreme values. In our first joint paper, we investigate a
sequence of functions which are the n-th derivatives of
Lebesgue's singular function with respect to its
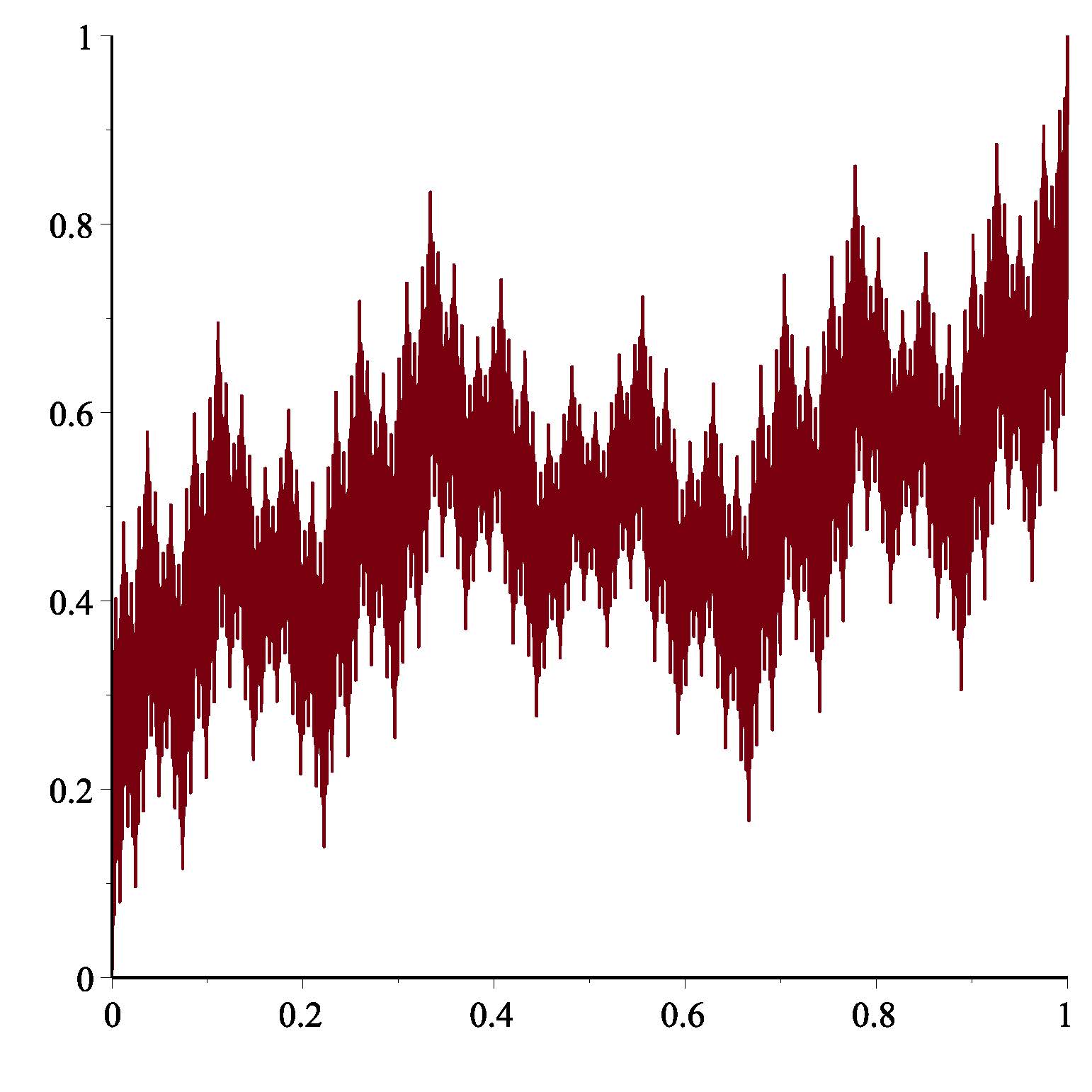
parameter. The first of these is Takagi's famous
continuous nowhere differentiable function (see the figure below). Our
paper extends several known results for the Takagi function to the entire
sequence of functions. The results (and conjectures!) we obtained for the sets
of maximum and minimum points of these functions are particularly intriguing.
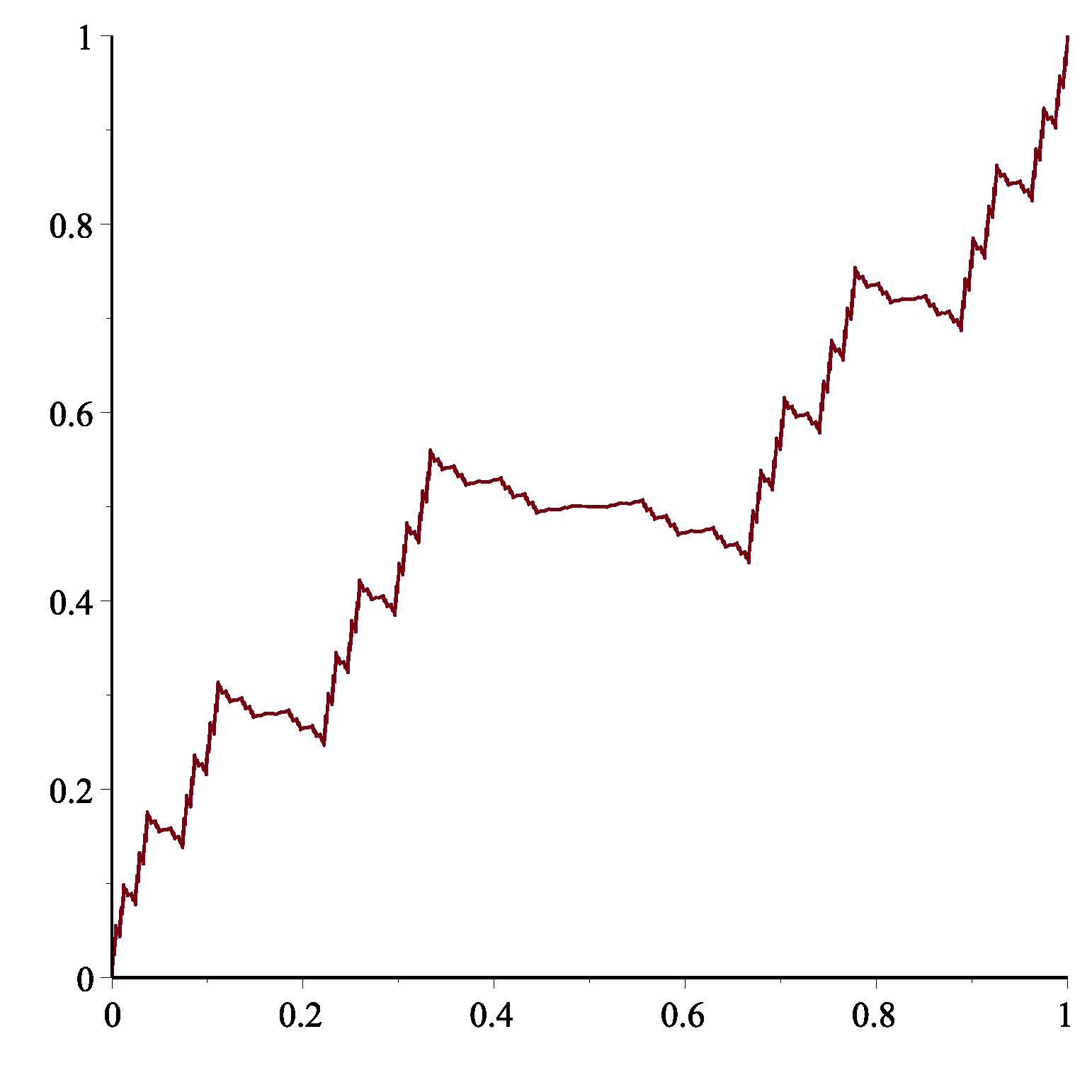
Other work we have done so far involves determination of the Hausdorff dimension
of the coordinate functions of space-filling curves, including Levy's dragon
curve and Polya's triangle-filling curves.


Takagi's nowhere-differentiable
function
Levy's dragon curve
I have also written several papers on the level sets of the Takagi function and its generalizations, and, with Kiko Kawamura, a survey of the literature about the Takagi function and its generalizations and applications.
More recently I have been interested in Okamoto's self-affine functions and their generalizations. Okamoto's functions form a one-parameter family of self-affine functions that includes earlier examples of Perkins and Katsuura, as well as the classical ternary Cantor function (and, much less interestingly, the identity function). The parameter a controls the shape and differentiability of the function F, as shown by Okamoto in 2006. When a > 2/3, F is nowhere differentiable (as shown below left for Perkins' function). At a = 0.5592 (see graph below right), another phase transition takes place: F changes from being differentiable almost everywhere (for a < 0.5592) to being differentiable almost nowhere (for a > 0.5592). The critical value .5592 is the solution (rounded to 4 decimal places) of a certain cubic equation.
Okamoto's function with a =5/6 (Perkins' function) Okamoto's function with a = 0.5592
One of my contributions was to compute the Hausdorff dimension of the
sets of exceptional points for the almost-everywhere (or almost
nowhere) differentiability, and to characterize the set of points where
Okamoto's function has an infinite derivative. This last result led me, unexpectedly, to the study of beta-expansions.
I have also investigated the differentiability of more general self-affine functions on an interval, and computed their pointwise Holder spectra. And, with my recent Ph.D. student Taylor Jones, I studied randomized versions of Okamoto's functions. We computed the box-counting dimension of their graphs and determined their differentiability properties.
You have an asset for sale (a house, say), and bids on the asset are made one
at a time. When do you decide a bid is large enough to accept it? Or, you are
playing the stock market and are wondering what the best time is to sell a stock
or exercise an option. The above questions (and countless others) belong to the
realm of Optimal Stopping Theory. They fit the
following general framework: An observer (often called gambler, or
statistician) is presented with a sequence of random variables (called
observations). After seeing each observation, the gambler must either accept
or reject it, without knowing the values of future observations. The goal is to
maximize the expected value of (some function of) the observation which is
finally accepted. The random variables may be either independent or dependent,
and their distributions may be either known or unknown to the observer. The time
horizon could be either finite or infinite. In the latter case, a
cost-per-observation or discount factor is usually assumed, so that "time works
against the observer". The development of optimal stopping theory started around
1960 with papers by Chow, Robbins, Karlin, and others, and remains fully alive
today, though most modern optimal stopping problems are in continuous time and require techniques from stochastic calculus.
My research in optimal stopping has focused on two types of problems. The first
area is optimal stopping of correlated random walks and
other directionally reinforced processes. The motivation for this work
(part of which has been done jointly with Michael Monticino) is to develop
optimal buy/sell rules for simple models of stock price movements which include
momentum. Some of our results have been fairly straightforward adaptations of
classical optimal stopping results for random walks, but others have required
substantially new ideas as well as a more in-depth analysis.
The second area involves prophet inequalities and
prophet-type inequalities. The goal in prophet problems is to compare the
optimal expected return of a gambler with that of a prophet, or player having
complete foresight into the future. The expected return of the prophet, which is
simply the expected maximum of the observations, can be viewed as an extreme
upper bound for the optimal expected return of a player who has some
(limited) foresight, e.g. a well-connected investor who has inside information
which allows him to partially predict the future. My main contributions to this
area concern sequences of random variables with arbitrary discount factors (both
random and deterministic). But I am also interested in how other types of
foresight affect the optimal stopping value, e.g. knowledge of the number of
available observations, or knowledge of the distributions of the random
variables. Another paper I wrote involves prophet inequalities and
prophet-type inequalities for observations arriving at random times. This
setting is more natural than the traditional discrete-time setting, but for
various reasons the problems become significantly more difficult to solve.
In average-optimal stopping, the distributions of
the random variables are assumed to be unknown, and the goal is to find a
stopping rule that performs best on the average over all possible
distributions. In such problems, one may think of Nature choosing (or
constructing) a distribution at random according to some scheme. One popular
construction of random probability distributions
was given by Dubins and Freedman in 1967. In one of my papers, I devised a
method for recursively computing the moments of the (random!) mean of a Dubins-Freedman
random distribution. From them, the distribution of the mean, which plays an
important role in statistical applications, can then be estimated.
In the past, I have done some work on the
Significant
Digit Phenomenon, an empirical law which says
that more numbers in the universe start with a low digit than with a higher
one. More precisely, the fraction of numbers having first significant digit
k is given by the log-base-10 of (k+1)/k. Thus, 30.1% of all numbers
in the universe have first significant digit 1, 17.6% have first digit
2, and so on. This curious phenomenon was first observed in 1881 by the
astronomer Simon Newcomb, who noticed that the first pages of logarithmic
tables wore out faster than later ones. It was rediscovered
in 1937 by physicist Frank Benford, who gathered strong empirical evidence
for the logarithmic law of significant digits, known today as
Benford's
Law: Benford collected 20.000 numbers from 20 different
sources including surface areas of rivers, baseball statistics, molecular
weights, street addresses of American Men in Science, and numbers found
on the front pages of newspapers. The first digit frequencies of these
numbers were amazingly close to the frequencies predicted by the logarithmic
law.
Though empirically firmly established by Benford's
experiments (and by later findings), there has been no convincing physical or
mathematical explanation for the Significant
Digit Phenomenon. Several explanations
have been proposed, including arguments based on scale- and base-invariance,
extensions of the notion of natural density, and picking a probability
distribution at random. However, none of these arguments have been fully
convincing.
Here is an intriguing fact about numbers that follows from the logarithmic law:
if you'd collect - each day for a period of say, ten weeks - all numbers on the
front page of the morning paper; then shift the decimal stop in each number to
the place right after the first significant digit (to get numbers between 1 and
10); and finally compute the 9 sums of all numbers in your data set having first
digit 1, all those having first digit 2, and so on..., you'd get nine approximately
equal sums. This observation can be made mathematically precise, and, when
extended to sums of numbers whose first k digits match (k>=1),
completely characterizes the logarithmic law. This was the result of my
Master's thesis and my first publication.
Ranges of vector measures
Lyapounov's celebrated convexity theorem of
1940 states that the range of an atomless vector measure is both convex and
compact. This extraordinarily elegant but deep and powerful result (or later
extensions of it) has been applied to such diverse areas as Banach space theory,
control theory, optimal stopping theory, game theory, fair division theory,
statistical decision theory, economics, graph theory, and logic. One extension
of Lyapounov's theorem, due to Dvoretzky, Wald and Wolfowitz, states that the
partition range of an atomless vector measure is convex and compact. For
both the range and the partition range, convexity typically fails if the vector
measure has atoms. J. Gouweleeuw and A. Dvoretzky have independently published
the same beautiful characterization of those vector measures whose range is
convex. In my Ph.D. dissertation, I took a different view and derived a sharp
bound on how far from convex the partition range of a vector measure can be,
given the size of the largest atom. This deep result combines several ideas from
convex geometry, measure theory, combinatorics and graph theory. In addition, I
sharpened some existing bounds (by J. Elton and T. Hill) on the non-convexity of
the range and the matrix range of a vector measure with atoms. These
bounds can be applied to determine worst-case deviations from optimality in a
variety of applications, most notably in fair division theory.
Another result from my dissertation is an application of convexity of the
partition range to a problem in statistical decision theory. Suppose a
continuous distribution is known up to a location parameter μ. A list of
n possible parameter values is given. You may take one observation X,
and must then guess which of the n given values is the true parameter
μ. The goal is to minimize the maximum risk - that is, the largest of the
n probabilities, under each of the possible parameter values, of guessing
incorrectly. This problem can be rephrased as an optimal-partitioning problem:
you would divide the real line into n intervals and declare that μ
is equal to the i-th value in the list, if X falls in the i-th
interval of the partition. The key to finding the worst possible minimax risk
(given some constraint on the spread of the distribution) is to cleverly
construct a number of preliminary partitions, and find the unique convex
combination with equal coordinates of the corresponding points in the partition
range. By convexity, this point belongs to the partition range as well, and the
corresponding partition of the real line is the one we want.