About Me


I am a graduate student at the University of North Texas, studying algebra. More specifically, I am researching invariant polynomials in a modular setting.
I received my B.S. from University of Texas at Austin, where my focus was on math education. After working at a high school, I realized I loved teaching, but was also interested in research! After attending many seminars my first semester at UNT, I realized Algebra was what fascinated me.
When not working on school or research, I enjoy spending time with my two dogs, painting with acrylics, travelling or playing strategy games. I also am an avid reader of science fiction and fantasy. I often delve into other genres, such as dystopian fiction, but those are my main source of enjoyment. My favorite place to travel to is Italy, but Germany is a close second. The picture is of me at the Musée des Arts et Métiers in Paris!
You can email me at ChelseaDrescher@my.unt.edu.
Mathematical Interests
I work in modular invariant theory and combinatorics. Here, modular means the underlying field has bad characteristic, or you can think of it as working modulo a bad prime. The polynomial rings I work in are generally over finite fields, such as a field of order 3. This means that 3x2+5x+1=2x+1 in this polynomial ring, since we are working mod 3. Students everywere can now rejoice, because we have that in this polynomial ring (x+y)3=x3+y3.
A group, such as the general linear group, may act on the polynomial ring, transforming the variables. For instance, one matrix might send x to 2x. In this case, the polynomial 2x+1 would be transformed into 2(2x)+1=4x+1 which becomes x+1, since we are working mod 3. If we have two variables x and y, then one group element could send x to x+y. In this case, the binomial theorem would be very useful for these types of actions if we have polynomials of high degree. But many of the coefficients may secretly be 0! How can we tell?
One beautiful theorem, called Lucas' theorem, gives a formula for binomial coefficients simplifying the process of figuring out when a binomial coefficient is 0 modulo a prime p. Here is the statement of the theorem:
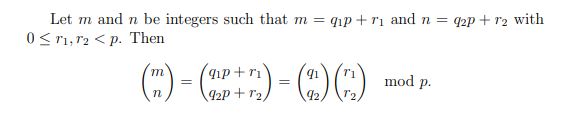
Say we want to expand the polynomial (x+y)14, and we want to know the coefficient of the term x5y9. The combination of the binomial theorem and Lucas's theorem tells us that the coefficient is
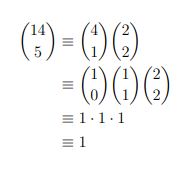
Compare that to finding the coefficient by hand without Lucas' theorem!