Anne Shepler

*Anne V. Shepler*
$Photo$	A mathematician is a blind man in a dark room searching for a black cat which isn't there. ---Charles R. Darwin	He didn't live long enough to see my mathematical vindication. ---H.S.M.Coxeter on E.C. Escher	Associate Professor of Mathematics University of North Texas Office: General Academic Building 471B Mailing Address: University of North Texas Mathematics Department 1155 Union Circle #311430 Denton, Texas, USA 76203-5017 Phone: (001) 940-565-4943 Fax: (001) 940-565-4805 E-mail: ashepler $AT$ unt.edu

Why does the mirror reflect you left-right, and not up-down? Coxeter, Ludwig Wittgenstein, and E.C. Escher....

ALGEBRA SEMINAR
TORA = Texas-Oklahoma Representations and Automorphic forms
I'm on the steering committee and organizer for a new conference series supported by the National Science Foundation
and Oklahoma State University, University of Oklahoma, and University of North Texas:

TORA I meeting: September 17--18, 2011, Univeristy of North Texas. (Plenary speakers: Nils Skoruppa, Sol Friedberg, Martin Raum.)
TORA IV meeting: March 23--24, 2013, University of North Texas. (Plenary speakers: Ken Ribet, Nolan Wallach, Susie Kimport.)

Special Session: "Combinatorial Avenues in Representation Theory"
Nathaniel Thiem, Richard Green, and I are organizing a Special Session conference at the American Mathematical Society meeting in Boulder, Colorado, April 13--14, 2013.

MATHEMATICAL RESEARCH

My work combines ideas in Algebra, Geometry, Invariant Theory, Representation Theory, and Combinatorics. Recently, I've been working in homological algebra, examining deformation theory, cohomology, and Drinfeld Orbifold Algebras (which include symplectic reflection algebras, rational Cherednik algebras, graded Hecke algebras, Drinfeld Hecke algebras, Weyl algebras, universal enveloping algebras, and twists by a group action or quantum parameters). Why? Physicists often regard space as a Calabi-Yau manifold endowed with symmetry. We model the local setting with a finite group G acting linearily on a finite dimensional vector space V. We mod out by the symmetry and regard the orbifold V/G. The coordinate ring is the ring of invariant polynomials k[V*]^G. The orbifold V/G may have singularities and one seeks geometrically to replace V/G with a smooth variety. Hochschild cohomology recommends an algebraic approach: replace the ring of invariant polynomials with the natural semi-direct product algebra k[V^*]#G (a skew group algebra). Hochschild cohomology governs the deformation theory of k[V^*]#G and predicts various algebras important in representation theory, combinatorics, and geometry of orbifolds.

I have a special interest in reflection groups. These are groups (acting on a finite dimensional vector space) generated by reflections: elements that fix a hyperplane (or "mirror") pointwise. They include the Weyl and Coxeter groups, complex reflection groups (u.g.g.r.'s), and reflection groups over arbitrary fields. Topics include invariant theory, arrangements of hyperplanes, regular polytopes, Hecke algebras, coinvariant algebras, Coxeter groups, Shephard Groups, and Braid groups. (Scott Crass can explain relations with Dynamical Systems.)

My work has been supported by several organizations:
        National Science Foundation:
            Research Grant (DMS-1101177), Principal Investigator, 2011--2014
                  Research Grant (DMS-0800951), Principal Investigator, 2008--2011
                  Research Grant (DMS 0402819), Principal Investigator, 2004--2008
            N.S.F. Post-Doctoral Research Fellowship (Award 9971099), Principal Investigator, 1999--2002
                  TORA Conference Grant (DMS-1132586), Co-Principal Investigator, 2011--2012
                  TORA Conference Grant (DMS-1302770), Co-Principal Investigator, 2013--2014
        National Security Agency: Young Investigators Research Grant, Principal Investigator, 2002--2004
        Alexander von Humboldt Foundation: Research Fellowship (at RWTH Aachen University), 2009
        Texas Coordinating Board: Advanced Research Program Grant ($43,469), PI, 2008--2010.

PUBLICATIONS

TALKS

GRADUATE STUDENTS      Masters/Ph.D. Advisor for:
    Paisa Seelungawat
    (B.S. from MIT, M.S. from UNT, currently Ph.D. student at Univ. of South Carolina),
    Briana Foster-Greenwood
    (B.S. from UNT, Ph.D. from UNT expected summer 2012.)
    Christine Uhl
    (Current Ph.D. student at UNT.)

Workshop on Algebras
Joint workshop on algebras, deformation theory, representation theory for and by postdocs/Ph.D. students from Texas A&M University, Baylor University, University of North Texas.

Conference on Hecke Algebras
Matt Douglass and I are organizing a special session on Hecke Algebras and Deformations in Geometry and Topology at the AMS meeting in St. Paul, Minnesota, April 10-11, 2010.

GAP You want Chevie with linux? No, you can't use gap4. Yes, you must install gap3r4p4. Doesn't compile?

PERSONAL
I attended the honors college at Valparaiso University---a small, liberal arts school in Indiana. I minored in the humanities, co-founded a comedy troupe, participated in many theatre productions, and worked for the music department as a piano accompanist. I decided to major in math after participating in an Research Experience for Undergraduates program at the University of Oklahoma. I also spent a semester at Hangzhou University in China (took Chinese language classes and also taught English at the Y.M.C.A.). Afterwards, I moved to California for grad school and scuba diving. Moray eels provide nice examples for constructing orbifolds. Maybe not wolf eel.

Hyperbolic Space: Reflection groups and modular forms:

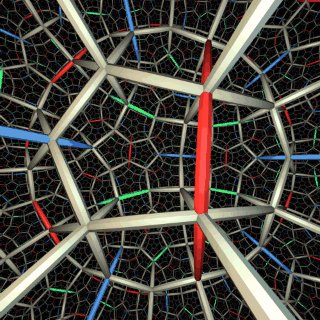
$Notknot$ $circle limit 3:$

Images by Douglas Dunham (University of Minnesota at Duluth), and Charlie Gunn with The Geometry Center (University of Minnesota).

Coxeter says of Escher's print: "He got it absolutely right to the millimetre, absolutely to the millimetre. ... Unfortunately, he didn't live long enough to see my mathematical vindication."

Site Meter